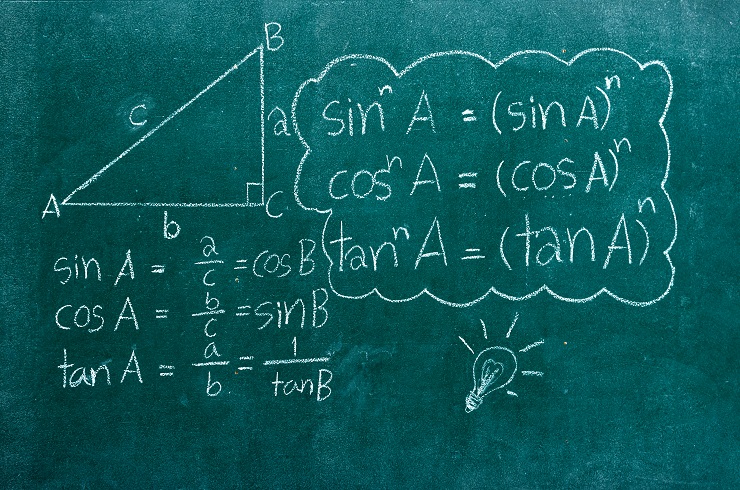Mathematical thinking is a fundamental skill that can be used across all kinds of disciplines and career paths. Whether you’re interested in going into the sciences, business, finance, or any other field, proficiency in mathematics can help you succeed. This guide will give you an overview of the different types of math tests that are commonly given during job interviews. It covers everything from arithmetic to algebra, geometry, probability theory and statistics. There are multiple sections in this article that can be read individually. However, we recommend reading it all from start to finish for the best understanding of how these topics relate to each other and how they could potentially be tested during an interview if you are an aspiring candidate for a job in accounting, finance or analytics fields.
Mathematics: The Basics
We live in a world of numbers. From measuring your waistline to analyzing statistics, numbers are everywhere. You may not feel it right away, but once you start looking for them you will see numbers almost everywhere. We use numbers in our daily lives so often that most people never think about what they actually mean or how they are used. But, if you take the time to understand them and how they impact the world around you, it can be quite fascinating. With that said, here is an introduction to math for beginners.
Measurement and Calculation
Most people think that math is simply a set of rules and formulas to calculate numbers. However, the real definition of math is “the study of quantity”. This is because the real essence of math is to measure and calculate the number of things. When we use math in our daily lives, we are essentially measuring and calculating the size, quantity, and amount of things. For example, when we measure the length of a table, we are essentially measuring the length of the table. This might seem like a very basic concept, but it’s important to know the difference between math and numbers because the two are often confused.
Fundamental Math Skills
Several mathematical skills are important for any beginner to know.
- Basic Calculations: This is the most basic math skill. Knowing basic calculations will help you to perform daily tasks such as adding, subtracting, multiplying, and dividing numbers.
- Order of Operations: This is the process of organizing calculations. Calculations are often done in steps, and when you don’t follow the right order, it can lead to errors. The order of operations dictates the order in which you perform calculations.
- Significant Figures: This is the number of digits that are relevant in a calculation. For example, you might measure the length of a table, and the result is 16 feet and 11 inches. This means that the first digit after the decimal point is an 11, meaning there are 11 1/2 inches between the two numbers.
- Basic Measurements: This refers to knowing the standard measurements of various things such as the length of an inch or the weight of a pound.
Basic Math Vocabulary
- Addition: This is the process of adding numbers or quantities together. For example, if you add the numbers 1 + 1, you get 2.
- Subtraction: This is the opposite process of addition. If you subtract the numbers 3 − 2, you get 1.
- Multiplication: This process involves multiplying two or more numbers together. For example, if you multiply 5 × 2, you get 10.
- Division: This is the opposite process of multiplication. If you divide the numbers 10 ÷ 2, you get 5. – Remainder: This is the remainder of a division calculation. For example, if you divide 10 by 2 and get 5 with a remainder of 5, this means the number 10 is divisible by 2 with 5 left over.
- Square: This means to multiply a number by itself, such as 3 × 3. Squaring a number can double its value.
- Cube: This means to multiply a number by itself two times, such as 2 × 2 × 2. Cubing a number can triple its value.
- Factorial: This is the process of multiplying all the numbers in a set of numbers, from 1 to a certain number. For example, 3! means 3 × 2 × 1.
- Absolute Value: This is the distance between two numbers, regardless of the numbers’ sign or direction. For example, 3 + 3 = 6, but 3 − 3 = 0.
Numbers in the Real World
The best way to learn math is to understand how it is used in the real world. When you take the time to understand the context of math, it can be a lot more interesting and useful.
- Making Change: This is one of the most common examples of using math in daily life. If you buy groceries using a $20 bill and get $19 change, you are essentially doing a mathematical calculation. You are determining how much change you need to give the cashier given the amount you have.
- Making Budgets: Many people use math to manage their finances and make budgets. You can use math to determine how much money you need to make your desired amount of purchases and still make a profit.
- Finding Discounts: Many stores and businesses offer discounts on certain items. You can calculate how much you need to spend to get the discount.
- Finding Equations: You can use math to find many different types of equations and formulas. For example, you can use math to find the equation for the area of a rectangular room.
- Finding Patterns: Math can also be used to find patterns in daily life. For example, you can use math to find the average temperature in a city during a certain period.
- Finding Ratios: This is the relationship between two quantities. For example, the ratio of boys to girls in a class is 2:1.
- Calculating Statistics: This is a collection of numerical data that describes a particular group. For example, you might want to find the statistics on the percentage of people who play baseball.
Advanced Math Skills
- Geometry: Geometry is the study of shapes and how they relate to each other. Most shapes are used in buildings, machines, and other important pieces of infrastructure.
- Algebra: Algebra is a type of math that is used to solve unknown quantities. For example, you might find that you need to solve for x or y.
- Calculus: Calculus is a branch of mathematics that primarily deals with rates of change. For example, you might want to find the rate at which a car travels.
- Logarithms: Logarithms are a type of math that is used to simplify mathematical calculations. For example, you might want to simplify the following equation: 10 × 100 = 1000.
- Probability: This is the chance that something will occur. For example, you might want to know how likely it is that the Chicago Cubs will win the World Series.
Summary
The world runs on math. Having a basic understanding of it will help you to make sense of the world around you and see how numbers impact your daily life. It also provides a great skill for the future, as almost all jobs require some knowledge of math. Being able to understand and apply math to your daily life can be very beneficial.
Statistics Problems
In statistics, problems that challenge your problem-solving skills usually involve numbers and probability. If you’re reading this article, it means you might have found one of those problems a little challenging – or at least a little trickier than you’d expected. Not to worry! Even the best stats students can struggle with statistics problems from time to time. To help get you back on track, we’ve outlined some of the most common issues that students come across when tackling these tricky statistical conundrums.
The Discrete Random Variable Problem
A problem that often comes up when tackling the problem of standard deviation is the discrete random variable problem. The problem occurs when the standard deviation is being calculated for a discrete data set, rather than a continuous one. A discrete data set is broken down into distinct categories or groups, while a continuous data set is made up of measurements that are recorded as an ongoing range of values, such as the heights of a given population. Let’s say you have a data set that records the amount of time each of your team members spends on each project they work on during a given week. Because the time each team member spends on each project will vary, the data set is discrete rather than continuous. This means that you will have to calculate the standard deviation differently from the way that you would for a continuous data set.
The Interpretation of Coefficients Problem
The problem of coefficients is often overlooked in the interpretation of results, but it is a very important feature of a regression analysis. Coefficients provide you with the impact that one variable has on another, i.e. a change in one variable has on another variable’s value. For example, when you are analyzing how job satisfaction impacts productivity, you usually take the job satisfaction variable and plug it into the equation. The coefficient is the impact that a change in job satisfaction has on productivity. Let’s say that you calculated the coefficient to be -0.3. This means that if job satisfaction increases by 10%, productivity will decrease by 3%. So, when you are reading through your results, you will want to make sure and note which variable is the “X” variable and which is the “Y” variable, as well as their coefficient if it is there.
The Scoring Problem
The scoring problem occurs when you have a test score that is not continuous, such as a test score out of 100 but is instead broken down into several discrete categories (such as pass/fail). To find the mean of the test score, you must first find the total number of points out of 100 that the test-takers scored. Let’s say that you have a group of students who took a test and all scored a different number of points between 1 and 100. You want to find the mean test score of the group of students, but you don’t have a continuous score. To find the mean, you must first add up all of the scores. So, if 5 students scored a 1, 2, 5, 7, and 100 points, their total score is 5+2+5+7+100 = 118. Next, you divide that total by the number of students, which is 5 in this case, to find the mean test score, which in this example is 28.8.
The Sampling Error Problem
The sampling error problem occurs when you are conducting a survey where you ask a sample group of people to respond to a question (i.e. how often do you go to the gym each week?). By choosing a sample group of people to respond to the question and then calculating a mean for the survey results, you are attempting to generalize that sample group’s response to the entire population (i.e. everyone who goes to the gym each week). The problem is that the response of your sample group may not be representative of everyone in the population. People who respond to the survey may have different ages, backgrounds, and levels of health, which may impact the way they respond to the question. Let’s say that you ask a sample group of people how often they go to the gym each week. You find that the mean response of the sample group is 3.5 times per week. You would like to generalize this result to the entire population of people who go to the gym each week. However, because your sample group is not representative of the entire population, the mean of 3.5 is not a good estimate for the entire group. The best way to find a more accurate mean for the entire population is to conduct a new survey with a more representative sample group.
The Confounding Variable Problem
When conducting a regression analysis, you want to make sure that you are not including any confounding variables in your equation. A confounding variable is something that impacts both the independent and dependent variables, which means that it will impact the results of your regression analysis. For example, if you are analyzing how age and job satisfaction impact productivity, you will want to make sure that gender is not added to the regression equation because it is a confounding variable. If you include gender in your regression analysis, you are ignoring the fact that gender is impacting both the independent and dependent variables. If you are conducting an analysis in which you want to isolate the impact that one variable has on another, you need to be careful not to include any confounding variables in your analysis. One way to do this is to run two separate regression analyses: one with the confounding variables and one without. Then, you can compare the results of each regression analysis to see how they differ. If they are significantly different, then you know that you have eliminated any confounding variables.
Summary
It can be challenging to wrap your head around statistics and probability problems. While they are important to learn, it’s easy to get overwhelmed with the amount of information you need to process. If you’re struggling with these problems, the first thing to do is to take a step back. Identify the problem that you’re facing and then break it down into smaller pieces. Look at examples of how others have solved similar problems to get a clearer picture of how to solve this one. With these common issues in mind, you can tackle any statistics problem that comes your way.
The Story Calculus
Calculus is one of the most important innovations in mathematics. It’s a branch of mathematics that deals with rates of change and their derivatives. In other words, it helps us understand how things change — how fast they’re going and in what direction they are headed. Calculus is used in almost every field of science, from physics to biology to computer science. In this section, you will learn about who invented calculus, its history, its advantages, and its applications. Read on for fascinating new details about this mathematical marvel.
What is Calculus?
Calculus is a branch of mathematics that deals with rates of change and their derivatives. A derivative is the rate at which something increases or decreases. In other words, it helps us understand how things change — how fast they’re going and in what direction they are headed. Calculus is used in almost every field of science, from physics to biology to computer science. Calculus is especially important in economics, management, and finance, where it is used to predict how changes in one factor will affect other factors. As an example, let’s say you want to open a pizzeria. Calculus can help you predict how many pizzas you’ll need to sell per day. It can also help you predict how changes in other factors — like the weather — will affect sales. Calculus helps us make better decisions by helping us understand the world around us. It allows us to take the world apart and understand its individual components. And then it allows us to put these components back together to form a new and more complex understanding of the world.
Who invented calculus?
Calculus was invented by Isaac Newton and Gottfried Wilhelm Leibniz. Newton is one of the most famous scientists in history. He made huge contributions to physics, astronomy, and mathematics. He also developed a branch of mathematics called differential calculus. Leibniz also came up with a new branch of mathematics. He called it integral calculus. But he came up with it independently of Newton — despite the fact that both men worked on the problem at the same time.
A brief history of Calculus
A brief history of Calculus 1544-1619 : Gottfried Wilhelm Leibniz was born in Germany in 1646. He was raised in an intellectual family. His father was a librarian, and his mother was a philosophy scholar. When Leibniz was 20, he was attending a meeting in Berlin when he heard a presentation about a new invention. It was a calculator — a mechanical device that could add numbers faster than a human being. Leibniz was very interested in this invention and spent some time studying the way this machine worked. He tried to create a new machine that could do more than just add numbers. He tried to create a machine that could do arithmetic and algebraic equations. However, he never came up with anything that worked perfectly. When he was 30, he started working on a new branch of mathematics. It was more complex than arithmetic and algebraic equations. 1636-1727 : Isaac Newton was born in England in 1642. He was an extremely intelligent child. His mother, who was a very religious woman, was afraid that he would lose his interest in religion and focus on science. To avoid this, she kept him away from books and schooling. As a result, Newton was not formally educated until he was 20. By that time, he had already started working on his inventions. When he was 26, he started working on a new branch of mathematics called differential calculus. In the same year, he published the first of his Mathematical Principles of Natural Philosophy, or the Principia, a book that revolutionized the field of physics.
Why is Calculus important?
Calculus is important because it lets us break things down into smaller pieces and then put them back together again. This is extremely useful in real-world situations. Calculus helps us make better decisions by understanding the world around us. It allows us to take the world apart and understand its individual components. And then it allows us to put these components back together to form a new and more complex understanding of the world.
Applications of Calculus
Basic Applications – Basic Applications – Calculus can help us understand how things change. It allows us to predict things like how long it will take to finish a project or how much money we’ll make on a business deal. – It can help us predict when a star will die or when an epidemic will break out. It can also be used to predict where a spacecraft will land on an alien planet. Business Applications – Business Applications – Calculus can help us understand how supply and demand work or how changes in interest rates will affect the economy. It can also help us predict how changes in one part of a company’s business will affect other parts. For example, it can be used to predict how changes in advertising will affect sales.
Bottom line
Calculus is one of the most important innovations in mathematics. It’s a branch of mathematics that deals with rates of change and their derivatives. It helps us understand how things change — how fast they’re going and in what direction they are headed. Calculus is used in almost every field of science, from physics to biology to computer science. It helps us make better decisions by understanding the world around us. It allows us to take the world apart and understand its individual components. And then it allows us to put these components back together to form a new and more complex understanding of the world. If you want to learn more about how to use calculus to solve real-world problems, you can use the helpful tips in this article as a guide.
Word to the Wiser assumes no responsibility or liability for any errors or omissions in the content of this site. The information contained in this site is provided on an “as is” basis with no guarantees of completeness, accuracy, usefulness or timeliness.